Autodysocjacja wody

Autodysocjacja wody lub autoprotoliza wody – samorzutna autodysocjacja cząsteczek wody pozostających w stanie ciekłym. Proces ten ma duże znaczenie praktyczne – decyduje m.in. o zdolności wody do rozpuszczania substancji jonowych a stała równowagi tej reakcji stanowi podstawę skali pH.

Temperaturowa zależność iloczynu jonowego wody (przy stałym ciśnieniu absolutnym 25 MPa)

Ciśnieniowa zależność iloczynu jonowego wody (przy stałej temperaturze 25 °C)

Zależność iloczynu jonowego wody od siły jonowej (przy stałej temperaturze 25 °C). Stężenie w jednostkach mol/L NaCl.

Przebieg reakcji autodysocjacji wody:

H₂O + H₂O ⇌ H₃O⁺ + OH⁻

Stałe reakcji

Zaniedbując aktywności, stałą równowagi tej reakcji można zdefiniować wzorem:

$K_{dys,w}=\mathrm {\frac {[H_{3}O^{+}][OH^{-}]}{[H_{2}O]^{2}}}$

W warunkach standardowych ma ona wartość 3,23×10⁻¹⁸ co w praktyce oznacza, że jest ona bardzo silnie przesunięta w stronę substratu, czyli niezdysocjowanej formy wody. W idealnie czystej wodzie w warunkach standardowych stężenie jonów [H₃O]⁺ i [OH]⁻ wynosi ok. 10⁻⁷ mol/l.

Stała kwasowa dana wzorem:

K_a = K_eq[H₂O] = ([H₃O⁺][OH⁻])/[H₂O]

gdzie [H₂O] ≈ 55,6 mol/dm³

ma w warunkach standardowych wartość 1,8×10⁻¹⁶.

Podane powyżej wartości otrzymane są przy użyciu stężenia molowego wody. Wartości numeryczne tych stałych byłyby znacząco inne w przypadku użycia aktywności rozpuszczalnika zamiast jego stężenia, ponieważ aktywność czystego rozpuszczalnika jest w termodynamice chemicznej zwykle przyjmowana jako równa jedności, podczas gdy stężenie molowe czystej wody wynosi około 55,6 mol/l.

Iloczyn jonowy wody

W przypadku rozcieńczonych roztworów wodnych można przyjąć, że stężenie molowe niezdysocjowanej formy wody jest stałą, a aktywność czystego rozpuszczalnika wynosi 1. Obserwacja ta stanowi podstawę definicji iloczynu jonowego wody. Zaniedbując aktywności:

K_w = K_a[H₂O] = K_{(dys, w)}[H₂O]² = [H₃O⁺][OH⁻]

Wartość iloczynu jonowego wody w temperaturze pokojowej wynosi ok. 10⁻¹⁴.

Podobnie jak dla innych bardzo małych wartości wywodzących się z definicji stałej równowagi, jak iloczyn rozpuszczalności czy stała dysocjacji lub przy określaniu stężenia jonów hydroniowych oraz wodorotlenowych, wartość iloczynu jonowego podaje się jako −log₁₀K_w (p jest operatorem oznaczającym obliczenie −log₁₀):

pK_w = −log₁₀K_w

Wartość pK_w ≈ 14 (w temperaturze pokojowej).

W innych temperaturach/ciśnieniach

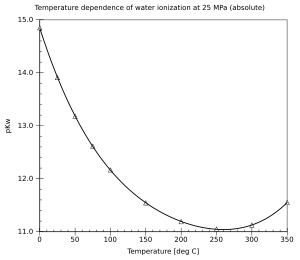
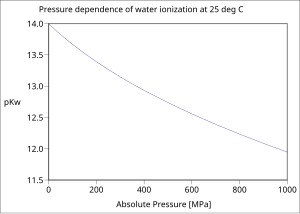
Przy normalnym ciśnieniu atmosferycznym woda jest ciekła w zakresie 0–100 °C. Wraz ze wzrostem temperatury dysocjacja staje się łatwiejsza (reakcja endotermiczna) i iloczyn jonowy K_w rośnie, a pK_w spada. Wartość pK_w zmienia się od ok. 14,95 w temperaturze 0 °C przez 14,0 (25 °C) i 13,0 (60 °C) do 11,25 w temperaturze 100 °C. W mniejszym stopniu, iloczyn jonowy wody zależy również od ciśnienia (zwiększona dysocjacja przy wyższym ciśnieniu). W warunkach podwyższonego ciśnienia, woda może pozostać ciekła aż do temperatury krytycznej. Iloczyn jonowy ciekłej wody zwiększa się ze zwiększającą się temperaturą aż do temperatury około 260 °C, a potem spada. Właściwości kwasowo-zasadowe wody w szerokim zakresie temperatur i ciśnień mają duże znaczenie praktyczne (na przykład, korozja w elektrowniach).

Związek z pH

Wartość pK_w ma kluczowe znaczenie dla definicji skali pH. Między pH i pK_w występuje zależność:

pH + pOH = pK_w

W idealnie czystej wodzie stężenia jonów [OH]⁻ i [H₃O]⁺ są sobie równe, stąd:

$\mathrm {[H_{3}O^{+}]=[OH^{-}]} ={\sqrt {K_{w}}}$

oraz (po zlogarytmowaniu obu stron):

pH = pOH = ½pK_w

Wartość pH = pOH w czystej wodzie, tzw. pH neutralne, wynosi 7,00 (25 °C, ciśnienie absolutne 100 kPa) i określa umowny środek skali pH_25 °C. Generalnie, wartość neutralnego pH zależy od temperatury (i w mniejszym stopniu od ciśnienia) i jest równe ½pK_w.