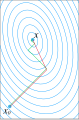
% A comparision of gradient descent and conjugate gradient (guess who wins)
function main()
% data
A=[17, 2; 2, 7]; % the matrix
b=[2, 2]'; % right-hand side
x0=[0, 0]'; % the initial guess
% linewidth and font size
lw= 2;
fs = 25;
% colors
red=[0.867 0.06 0.14];
blue = [0, 129, 205]/256;
green = [0, 200, 70]/256;
black = [0, 0, 0];
white = 0.99*[1, 1, 1];
% Set up the plotting window
figure(1); clf; set(gca, 'fontsize', fs); hold on; axis equal; axis off;
s = 0.16; x = A\b;
Ax = x(1)-s; Bx = x(1)+s; Ay = x(2)-2.0*s; By = x(2)+s;
plot([Ax Bx Bx Ax Ax], [Ay Ay By By Ay], 'color', blue, 'linewidth', lw/2); % plot a blue box
s=0.005; plot(Ax-s, Ay-s, '*', 'color', white); plot(Bx+0.5*s, By+0.5*s, '*', 'color', white); %markers
Box = [Ax Bx Ay By];
axis (Box);
% plot the contours of the quadratic form associated with A and b
plot_contours(A, b, Box, lw, blue);
% Do conjugate gradient and gradient descent.
% For the first one, start a bit shifted so that the two graphs don't overlap.
shift = 0.0015*[1, -1];
small_rad=0.002;
tol = eps;
x = conj_gradient(A, b, x0, tol, lw, red, small_rad, shift);
x = grad_descent (A, b, x0, tol, lw, green, small_rad);
% text
small = 0.015;
text(x0(1)-2*small, x0(2)-1.6*small, 'x', 'fontsize', fs);
text(x0(1)-0.5*small, x0(2)-3*small, '0', 'fontsize', floor(0.7*fs));
text(x(1)+small, x(2)+small, 'x', 'fontsize', fs);
% some balls for beauty
small_rad = 0.003;
ball(x0(1)+shift(1)/2, x0(2)+shift(2)/2, small_rad, blue)
ball(x(1), x(2), small_rad, blue)
% save to disk as eps and svg
saveas(gcf, 'Conjugate_gradient_illustration.eps', 'psc2');
plot2svg('Conjugate_gradient_illustration.svg');
function x = conj_gradient(A, b, x, tol, lw, color, small_rad, shift)
r=A*x - b;
d=-r;
while norm(r) > tol
% a pretty ball for beauty, to cover imperfections when two segments are joined
ball(x(1)+shift(1), x(2)+shift(2), small_rad, color);
alpha = -dot(r, d)/dot(A*d, d);
x0 = x;
x = x + alpha*d;
r=A*x - b;
beta = dot(A*r, d)/dot(A*d, d);
d0 = d;
d = -r + beta*d;
plot([x0(1), x(1)]+shift(1), [x0(2), x(2)]+shift(2), 'color', color, 'linewidth', lw)
end
function x = grad_descent(A, b, x, tol, lw, color, small_rad)
r=A*x - b;
d=-r;
while norm(r) > tol
% a pretty ball for beauty, to cover imperfections when two segments are joined
ball(x(1), x(2), small_rad, color);
alpha = -dot(r, d)/dot(A*d, d);
x0 = x;
x = x + alpha*d;
r=A*x - b;
beta = 0; %beta = dot(A*r, d)/dot(A*d, d);
d0 = d;
d = -r + beta*d;
plot([x0(1), x(1)], [x0(2), x(2)], 'color', color, 'linewidth', lw)
end
function plot_contours (A, b, Box, lw, color);
N=200; % number of points (don't make it big, code will be slow)
E = A\b; % the exact solution, around which we will draw the contours
B = 0.12;
[X, Y]=meshgrid(linspace(Box(1)-B, Box(2)+B, N), linspace(Box(3)-B, Box(4)+B, N)); % X and Y coordinates
% the quadratic form f= (1/2)*x'*A*X-b'*x;
f = inline('0.5*A(1, 1)*X.*X + A(1, 2)*X.*Y+0.5*A(2, 2)*Y.*Y-b(1)*X-b(2)*Y', 'X', 'Y', 'A', 'b');
Z = 0.5*A(1, 1)*X.*X + A(1, 2)*X.*Y+0.5*A(2, 2)*Y.*Y-b(1)*X-b(2)*Y;
% prepare to draw the contours
x0 = A\b; f0 = f(x0(1), x0(2), A, b);
No = 25; % number of contours
Levels = (linspace(f0, 1, No)-f0).^2+f0;
% Plot the contours with 'contour' in figure(2), and then with 'plot' in figure(1).
% This is to avoid a bug in plot2svg, it can't save output of 'contour'.
figure(2); clf; hold on;
for i=1:length(Levels)
figure(2);
[c, stuff] = contour(X, Y, Z, [Levels(i), Levels(i)]);
[m, n]=size(c);
if m > 1 & n > 0
% extract the contour from the contour matrix and plot in figure(1)
l=c(2, 1);
x=c(1,2:(l+1)); y=c(2,2:(l+1));
figure(1); plot(x, y, 'color', color, 'linewidth', lw/2);
end
end
figure(1);
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, color);
set(H, 'EdgeColor', 'none');