Wikipedia

Fluorescencja parametryczna

nieliniowy proces optyczny
(Przekierowano z Spontaniczna parametryczna konwersja w dół)

Fluorescencja parametryczna (znana również jako spontaniczna parametryczna konwersja w dół, SPDC lub rozpraszanie parametryczne) jest nieliniowym natychmiastowym procesem optycznym, w który jeden foton o wyższej energii (tj. foton pompujący) przechodzi (ulega konwersji w dół) w dwa fotony o niższej energii, mianowicie w foton sygnałowy i foton uboczny (ang. idler), zgodnie z zasadą zachowania energii i zasadą zachowania pędu. Jest to ważny proces w optyce kwantowej do generowania splątanych par fotonów i pojedynczych fotonów.

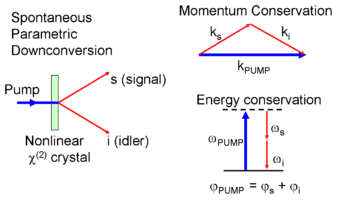
Schemat procesu fluorescencji parametrycznej; zasady zachowania energii i pędu dotyczą wenętrza kryształu

Proces podstawowy

edytuj
 
Schemat fluorescencji parametrycznej z wyjściem typu I
Film z doświadczenia pokazującego fluktuacje kwantowe (w czerwonym pierścieniu) wzmocnione przez fluorescencję parametryczną (nawiązującą do schematu wyżej)

Nieliniowy kryształ służy do rozdzielenia wiązek fotonów na pary fotonów, które mają energię i pęd (zgodnie z zasadą zachowania energii i zasadą zachowania pędu) równe energii i pędowi oryginalnego fotonu i sieci krystalicznej. Ponieważ współczynnik załamania zmienia się wraz z częstotliwością, tylko niektóre trójki częstotliwości będą dopasowane fazowo tak, aby można było jednocześnie zachować energię i pęd. Dopasowywanie faz najczęściej osiąga się przy użyciu dwójłomnych nieliniowych materiałów, których współczynnik załamania zmienia się wraz z polaryzacją.

Typy fluorescencji parametrycznej są uporządkowane według wzajemnych relacji polaryzacji trójki fotonów: fotonu wejściowego (pompy) i dwóch fotonów wyjściowych (sygnału i ubocznego), mianowicie:

  • jeśli fotony sygnału, foton uboczny oraz niszczony foton pompy mają taką samą polaryzację, proces nazywa się fluorescencją parametryczną typu 0[1];
  • jeśli fotony sygnału i uboczny mają tę samą polaryzację, ale są prostopadłe do polaryzacji fotonu pompującego, jest to fluorescencja parametryczna typu I.
  • jeśli fotony sygnału i uboczny mają polaryzacje prostopadłe do siebie, jest to fluorescencja parametryczna typu II[2].

Wydajność konwersji fotonów we fluorescencji parametrycznej jest zazwyczaj bardzo mała (najwyższą wydajność, rzędu 4 par fotonów na 106 przychodzących fotonów osiągnięto w falowodach z periodycznie spolaryzowanego przekładańca z niobianu litu (z ang. PPLN)[3]. Jednakże jeżeli jedna połowa pary tj. sygnał zostaje wykryty w dowolnym momencie, wtedy wiadomo, że jego uboczny partner jest obecny. Zdegenerowana część wyjściowa oscylacji parametrycznej optycznego parametrycznego oscylatora typu I jest ściśniętą próżnią, która zawiera tylko parzyste liczby fotonów[4]. Zdegenerowane wyjście konwertera typu II jest dwumodową ściśniętą próżnią.

Przykład

edytuj
 
Schemat fluorescencji parametrycznej z wyjściem typu II

W standardowej aparaturze używanej do fluorescencji parametrycznej silna wiązka laserowa, zwana wiązką pompującą, jest skierowana na kryształ BBO (boran baru). Większość fotonów przechodzi przez kryształ, czasami jednak niektóre fotony spontanicznie ulegają fluorescencji parametrycznej typu II, w której powstałe dwa fotony są wzajemnie prostopadłe a ich trajektorie są ograniczone krawędziami dwóch odpowiednich stożków, których osie są rozmieszczone symetrycznie względem wiązki pompującej. Ponadto, ze względu na zachowanie pędu, dwa powstałe fotony są zawsze symetrycznie rozmieszczone względem wiązki. Co ważne, trajektorie pary fotonów mogą przebiegać dwoma liniami zawartymi w obszarze krzyżowania się obu stożków, co daje splątanie pary fotonów, które są spolaryzowane prostopadle do siebie[5][6].

Kryształ KDP (diwodorofosforanu potasu)(inne języki) jest najczęściej używany do fluorescencji parametrycznej typu I, w której oba fotony mają tę samą polaryzację[7].

Historia

edytuj

Luminescencja parametryczna została opisana już w 1970 r. przez D. Kliszko, A. N. Penina, B. F. Polkownikowa[8], oraz D. C. Burnhama and D. L. Weinberga[9][10]. Po raz pierwszy została zastosowana doświadczalnie w badaniach nad zgodnością fazową fotonów przez dwie niezależne pary badaczy pod koniec lat 80. XX wieku: Carrolla Alleya i Yanhua Shih oraz Rupamanjari Ghosh i Leonard Mandela[11][12]. Stwierdzono dualizm między emisją częściowo zgodną fazową (twierdzenie Van Citterta–Zernike)(inne języki)) a emisją częściowo splątanej pary fotonów[13].

Aplikacje

edytuj

Fluorescencja parametryczna pozwala na tworzenie pól optycznych zawierających (w przybliżeniu) pojedynczy foton. Do 2005 r. była dominującym mechanizmem doświadczalnym do tworzenia pojedynczych fotonów (zwanych również jako stany Foka)[14]. Pojedyncze fotony oraz pary fotonów są często wykorzystywane w doświadczeniach obejmujących informację kwantową, próby Bella pozbycia się zmiennych lokalnych oraz w zastosowaniach takich jak kryptologia kwantowa.

Fluorescencja parametryczna jest szeroko stosowana do tworzenia par splątanych fotonów o wysokim stopniu korelacji przestrzennej[15]. Takie pary są stosowane w splątanym obrazowaniu duchów(inne języki), w którym informacje są łączone splątaniem z dwóch detektorów światła: konwencjonalnego detektora wielopikselowego, który nie widzi obiektu, oraz skanującego detektora jednopikselowego, który widzi obiekt, osiągając wysoki stosunek sygnału do szumu. Stosując rekonstrukcję obrazu można tworzyć wysokiej jakości obrazy obiektów na podstawie surowych danych ze średnio mniej niż jednym wykrytym fotonem na piksel obrazu[16].

Alternatywy

edytuj

Nowo zaobserwowany efekt emisji dwu-fotonów z półprzewodników zasilanych elektrycznie jest propozycją bardziej wydajnego źródła splątanych par fotonów (z emisją pary fotonów około 105 razy rzadszą niż spontaniczna emisja jednego fotonu)[17]. Inaczej niż we fluorescencji parametrycznej, fotony pary emitowanej z półprzewodników zwykle nie są identyczne, lecz mają różne energie[18]. Do niedawna zakładano w ramach błędnie poszerzonej zasady nieoznaczoności na zjawiska złożone, że para emitowanych fotonów tworzy się w tym samym miejscu, jednak nowy nielokalny mechanizm wytwarzania skorelowanych par fotonów pokazał, że fotony tworzące parę mogą być emitowane oddzielnie z innych przestrzennie oddzielonych punktów[19][20].

Przypisy

edytuj
  1. ↑ Stefan Lerch, Bänz Bessire, Christof Bernhard, Thomas Feurer i inni. Tuning curve of type-0 spontaneous parametric down-conversion. „Journal of the Optical Society of America B”. 30 (4), s. 953–958, 2013-04-01. DOI: 10.1364/JOSAB.30.000953. arXiv:1404.1192. ISSN 0740-3224. Bibcode: 2013JOSAB..30..953L. 
  2. ↑ Robert Boyd: Nonlinear Optics, Third Edition. New York: Academic Press, 2008, s. 79–88. ISBN 978-0-12-369470-6.
  3. ↑ Matthias Bock, Andreas Lenhard, Christopher Chunnilall, Christoph Becher. Highly efficient heralded single-photon source for telecom wavelengths based on a PPLN waveguide. „Optics Express”. 24 (21), s. 23992–24001, 17 October 2016. DOI: 10.1364/OE.24.023992. ISSN 1094-4087. PMID: 27828232. Bibcode: 2016OExpr..2423992B. 
  4. ↑ L.-A. Wu, M. Xiao, H.J. Kimble. Squeezed states of light from an optical parametric oscillator. „J. Opt. Soc. Am. B 4”. 1465, 1987. 
  5. ↑ P. Kwiat i inni. New High-Intensity Source of Polarization-Entangled Photon Pairs. „Phys. Rev. Lett.”. 75 (24), s. 4337–4341, 1995. DOI: 10.1103/PhysRevLett.75.4337. PMID: 10059884. Bibcode: 1995PhRvL..75.4337K. 
  6. ↑ The super-source and closing the communication loophole. W: Anton Zeilinger: Dance of the Photons: From Einstein to Quantum Teleportation. Farrar, Straus and Giroux, 12 October 2010. ISBN 978-1-4299-6379-4.
  7. ↑ M H A Reck, Quantum Interferometry with Multiports: Entangled Photons in Optical Fibers (page 115) [online] [dostęp 2014-02-16].
  8. ↑ Klyshko D. N., Penin A. N., Polkovnikov B. F., „Parametric Luminescence and Light Scattering by Polaritons”, JETP Lett. 11, 05 (1970).
  9. ↑ D.C. Burnham, D.L. Weinberg. Observation of simultaneity in parametric production of optical photon pairs. „Phys. Rev. Lett.”. 25 (2), s. 84, 1970. DOI: 10.1103/physrevlett.25.84. Bibcode: 1970PhRvL..25...84B. 
  10. ↑ D. Greenberger, M. Horne, and A. Zeilinger, „A Bell Theorem Without Inequalities for Two Particles, Using Efficient Detectors” (2005), note 18.
  11. ↑ Y. Shih and C. Alley, in Proceedings of the 2nd Int’l Symposium on Foundations of QM in Light of New Technology, Namiki et al., eds., Physical Society of Japan, Tokyo, 1986.
  12. ↑ R. Ghosh, L. Mandel. Observation of Nonclassical Effects in the Interference of Two Photons. „Phys. Rev. Lett.”. 59 (17), s. 1903, 1987. DOI: 10.1103/physrevlett.59.1903. PMID: 10035364. Bibcode: 1987PhRvL..59.1903G. 
  13. ↑ http://pra.aps.org/abstract/PRA/v62/i4/e043816 – Duality between partial coherence and partial entanglement.
  14. ↑ Alessandro Zavatta, Silvia Viciani, Marco Bellini. Tomographic reconstruction of the single-photon Fock state by high-frequency homodyne detection. „Physical Review A”. 70 (5), s. 053821, 2004. DOI: 10.1103/PhysRevA.70.053821. arXiv:quant-ph/0406090. Bibcode: 2004PhRvA..70e3821Z. 
  15. ↑ S.P. Walborn, C.H. Monken, S. Pádua, P.H. Souto Ribeiro. Spatial correlations in parametric down-conversion. „Physics Reports”. 495 (4–5), s. 87–139, 2010. DOI: 10.1016/j.physrep.2010.06.003. arXiv:1010.1236. ISSN 0370-1573. Bibcode: 2010PhR...495...87W. 
  16. ↑ Peter A. Morris, Reuben S. Aspden, Jessica E.C. Bell, Robert W. Boyd i inni. Imaging with a small number of photons. „Nature Communications”. 6, s. 5913, 2015. DOI: 10.1038/ncomms6913. arXiv:1408.6381. ISSN 2041-1723. Bibcode: 2015NatCo...6.5913M. 
  17. ↑ A. Hayat, P. Ginzburg, M. Orenstein, Observation of Two-Photon Emission from Semiconductors, Nature Photon. 2, 238 (2008).
  18. ↑ J. Chluba, R.A. Sunyaev. Induced two-photon decay of the 2s level and the rate of cosmological hydrogen recombination. „Astronomy and Astrophysics”. 446 (1), s. 39–42, 2006. DOI: 10.1051/0004-6361:20053988. arXiv:astro-ph/0508144. Bibcode: 2006A&A...446...39C. 
  19. ↑ Kayn A. Forbes, Jack S. Ford, David L. Andrews. Nonlocalized Generation of Correlated Photon Pairs in Degenerate Down-Conversion. „Physical Review Letters”. 118 (13), s. 133602, 2017-03-30. DOI: 10.1103/PhysRevLett.118.133602. Bibcode: 2017PhRvL.118m3602F. 
  20. ↑ Kayn A. Forbes, Jack S. Ford, Garth A. Jones, David L. Andrews. Quantum delocalization in photon-pair generation. „Physical Review A”. 96 (2), s. 023850, 2017-08-23. DOI: 10.1103/PhysRevA.96.023850. Bibcode: 2017PhRvA..96b3850F. 
Źródło: „https://pl.wiki.x.io/w/index.php?title=Fluorescencja_parametryczna&oldid=70536935”