Orbita oskulacyjna

Orbita oskulacyjna – keplerowska orbita obiektu, na której ten obiekt poruszałby się wokół ciała centralnego po ustaniu (w określonej chwili) perturbacji jego ruchu.

Porównanie orbity rzeczywistej i oskulacyjnej dla ruchu perturbowanego (różnice celowo wyolbrzymione). Kolor czarny – orbita oskulacyjna; czerwony – rzeczywista; szary – orbita ciała perturbującego

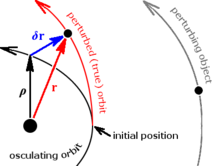
Rozwiązaniem zagadnienia dwóch ciał są orbity keplerowskie, będące krzywymi stożkowymi (elipsą, parabolą lub hiperbolą). Kształt, rozmiar i orientację w przestrzeni takiej orbity oraz położenie na niej ciała w chwili T można opisać podając sześć parametrów, określanych mianem elementów orbitalnych. Najczęściej są to półoś wielka (a) lub odległość perycentrum (q), mimośród (e), nachylenie (i), długość węzła wstępującego (Ω), argument perycentrum (ω) albo długość perycentrum ($\varpi$), oraz anomalia średnia w chwili T (M) lub moment przejścia przez perycentrum (T0). Elementy te są równoważne wektorom stanu orbitalnego (czyli wektorowi położenia i prędkości ciała) na określony moment czasu.

W przypadku, jeśli ruch ciała podlega perturbacjom, rzeczywista orbita ciała przestaje być keplerowską krzywą stożkową, a elementy keplerowskie przestają być stałymi ruchu. Dla każdej chwili t można jednak wyznaczyć elementy takiej orbity keplerowskiej, która jest ściśle styczna do orbity rzeczywistej w punkcie, w którym ciało się wtedy znajduje i która dokładnie odwzorowuje wektor położenia i prędkości ciała w tym punkcie. Elementy te nazywamy elementami oskulacyjnymi, a moment, na który zostały wyznaczone, nosi nazwę epoki oskulacji (łac. osculum – przelotny pocałunek). Orbitę oskulacyjną możemy też wyobrazić sobie jako taką orbitę keplerowską, po której poruszałoby się dalej ciało, gdybyśmy w chwili odpowiadającej epoce oskulacji "wyłączyli" wpływ wszystkich innych oddziaływań, z wyjątkiem oddziaływania ciała centralnego.

Wartości elementów oskulacyjnych są zmienne w czasie. W przypadku obiektów, których ruch jest tylko nieznacznie perturbowany (np. masywnych planet), zmiany te są niewielkie i rzeczywista orbita w niewielkim tylko stopniu odbiega od orbity keplerowskiej. Natomiast w przypadku ciał podlegających silnym perturbacjom (np. komet) zmiany te bywają bardzo duże, do tego stopnia, że np. oskulacyjna odległość apocentrum wyznaczona dla chwili, kiedy kometa poruszała się w pobliżu perycentrum, może być zupełnie różna, niż rzeczywista odległość, jaką kometa ta osiągnie w chwili największego oddalenia od Słońca.

Zobacz też

• prawa Keplera
• elementy orbitalne