Okrąg dopisany

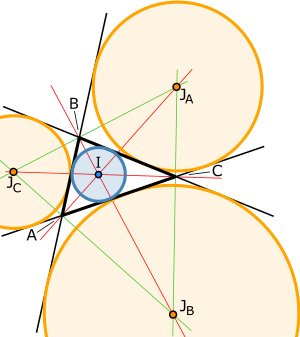
Okrąg dopisany do trójkąta – okrąg styczny do jednego z boków trójkąta i przedłużeń dwóch pozostałych boków. Jego środek znajduje się w punkcie przecięcia dwusiecznych odpowiednich kątów zewnętrznych. Okrąg ten ma dokładnie jeden punkt wspólny z trójkątem.

Na pomarańczowo zaznaczone są trzy okręgi dopisane do trójkąta ΔABC

Pole trójkąta

Przyjmując $r_{a}$ – promień okręgu dopisanego naprzeciw wierzchołka A oraz $a,b,c$ – boki naprzeciw odpowiednich wierzchołków, otrzymujemy wzór na pole trójkąta:

$S={\frac {1}{2}}r_{a}(b+c-a).$

Dowód

Po przedłużeniu boków $b$ i: $c$ oraz poprowadzeniu prostej stycznej do okręgu dopisanego przecinającej te przedłużenia odpowiednio w punktach $B'$ i: $C'$ uzyskujemy trójkąt $AB'C',$ dla którego jest to okrąg wpisany. Jest on również wpisany w czworokąt $BCC'B'.$ Pole trójkąta $AB'C'$ wyraża się wzorem:

$S={\frac {1}{2}}r_{a}(a'+b'+c'),$

a czworokąta:

$S={\frac {1}{2}}r_{a}(a+(b'-b)+a'+(c'-c)).$

Pole trójkąta jest różnicą tych pól.

Linki zewnętrzne

• Paweł Rudnicki, Okręgi dopisane trójkąta prostokątnego, Wrocławski Portal Matematyczny, matematyka.wroc.pl, 15 września 2018 [dostęp 2024-10-07].
• Eric W.E.W. Weisstein Eric W.E.W., Excircles, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-10-07].