Metoda różnic skończonych

Metoda różnic skończonych – metoda numeryczna rozwiązywania równań różniczkowych polegająca na przybliżeniu pochodnej funkcji ilorazami różnicowymi w zdyskretyzowanej przestrzeni.

Metoda różnic skończonych polega na dyskretyzacji funkcji na siatce.

Wzór na pochodną z szeregu Taylora

Przy założeniu, że istnieją pochodne danej funkcji $f(x)$ do $n$-tej pochodnej włącznie, można ją rozwinąć w szereg Taylora:

$f(x_{0}+h)=f(x_{0})+{\frac {f'(x_{0})}{1!}}h+{\frac {f^{(2)}(x_{0})}{2!}}h^{2}+\ldots +{\frac {f^{(n)}(x_{0})}{n!}}h^{n}+R_{n}(x)$

gdzie $R_{n}(x)$ - reszta. Przy ograniczeniu do drugiego wyrazu rozwinięcia mamy

$f(x_{0}+h)=f(x_{0})+f'(x_{0})h+R_{1}(x)$

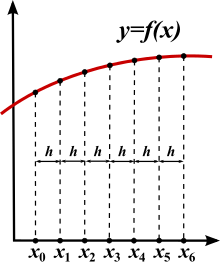
Jeżeli wyraz $R_{1}(x)$ jest dostatecznie mały, to pochodną funkcji w punkcie $x_{0}$ można przybliżyć ilorazem różnicowym

$f'(x+0)\approx {\frac {f(x_{0}+h)-f(x_{0})}{h}}$

Bibliografia

• Z. Fortuna, B. Macukow, J. Wąsowski, Metody numeryczne Podręczniki akademickie Elektronika, informatyka, telekomunikacja, Warszawa: Wydawnictwa Naukowo-Techniczne, 1982, s. 285–363.
• D. Potter, Metody obliczeniowe fizyki, fizyka komputerowa, Warszawa: PWN, 1982, s. 19–43.
• J. Szmelter, Metody komputerowe w mechanice, Warszawa: PWN, 1980, s. 205-232 (Rozdział 11. Metoda różnic skończonych).
• A. Ralston, Wstęp do analizy numerycznej, Warszawa: PWN, 1971.

Linki zewnętrzne

• Maszyna różnicowa, „DeltaMi” [dostęp 2018-10-27]  (pol.).
• Metoda różnic skończonych, [dostęp 2023-06-24] (pol.).
• WaldemarW. Wietrzykowski WaldemarW., net3plus – SymP • Maszyna różnicowa – komputer specjalizowany (część I) [online], net3plus.awardspace.com, s. 4–5 [dostęp 2018-10-23] [zarchiwizowane z adresu 2018-10-24]  (pol.).