Geometria sferyczna
Geometria sferyczna – geometria powierzchni kuli (czyli geometria sfery). Geometria ta była badana przez starożytnych Greków (Menelaos z Aleksandrii, Klaudiusz Ptolemeusz) ze względu na potrzeby nawigacji oraz astronomii[1].
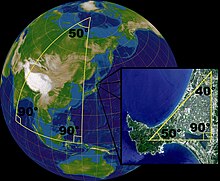
Geometria sferyczna jest przykładem geometrii nieeuklidesowej o stałej dodatniej krzywiźnie. Od geometrii eliptycznej różni się tym, że nie każde dwa punkty jednoznacznie wyznaczają prostą[2]. W szczególności prostymi w typowym „geograficznym” modelu geometrii sferycznej są koła wielkie sfery, a punkty antypodyczne nie wskazują jednoznacznie o które koło wielkie chodzi[3].
Metryką w tym modelu jest miara kąta o wierzchołku w środku sfery i ramionach przechodzących przez punkty dla których liczona jest odległość. Wymiar sfery (taki jaki płaszczyzny, o 1 mniejszy od wymiaru kuli) jest wymiarem geometrii sferycznej[4].
Przypisy
edytuj- ↑ Nowa encyklopedia powszechna PWN: Sud-żyz. Wydawnictwo Naukowe PWN, 2004, s. 320.
- ↑ Michel-Marie Deza, Elena Deza: Dictionary of Distances. Elsevier, 2006, s. 73.
- ↑ Arlan Ramsay, Robert D. Richtmye: Introduction to Hyperbolic Geometry. Springer Science & Business Media, 2013, s. 17.
- ↑ Geometria sferyczna. [dostęp 2015-08-03].
Linki zewnętrzne
edytuj- Spherical geometry (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].