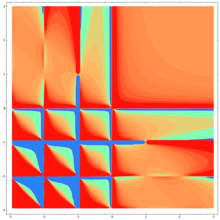
Funkcja Β (czytaj: funkcja beta ) zwana też całką Eulera pierwszego rodzaju – funkcja specjalna określona dla liczb zespolonych
x
,
y
,
{\displaystyle x,y,}
[1]
Wykres funkcji beta uzyskany techniką kolorowania dziedziny
B
(
x
,
y
)
=
∫
0
1
t
x
−
1
(
1
−
t
)
y
−
1
d
t
,
d
l
a
R
e
(
x
)
,
R
e
(
y
)
>
0.
{\displaystyle \mathrm {B} (x,y)=\int \limits _{0}^{1}t^{x-1}(1-t)^{y-1}\,dt,\quad \mathrm {dla} \quad Re(x),Re(y)>0.}
Funkcję Beta można również przedstawić w inny sposób:
B
(
x
,
y
)
=
Γ
(
x
)
Γ
(
y
)
Γ
(
x
+
y
)
,
{\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}},}
gdzie
Γ
{\displaystyle \mathrm {\Gamma } }
funkcja gamma .
Wynika stąd, że funkcja beta jest symetryczna, tj.
B
(
x
,
y
)
=
B
(
y
,
x
)
.
{\displaystyle \mathrm {B} (x,y)=\mathrm {B} (y,x).}
Postacie funkcji beta dla liczb rzeczywistych dodatnich
edytuj
B
(
x
,
y
)
=
2
∫
0
π
/
2
(
sin
θ
)
2
x
−
1
(
cos
θ
)
2
y
−
1
d
θ
,
Re
(
x
)
>
0
,
Re
(
y
)
>
0
,
B
(
x
,
y
)
=
∫
0
∞
t
x
−
1
(
1
+
t
)
x
+
y
d
t
,
Re
(
x
)
>
0
,
Re
(
y
)
>
0
,
B
(
x
,
y
)
=
∑
n
=
0
∞
(
n
−
y
n
)
x
+
n
,
B
(
x
,
y
)
=
x
+
y
x
y
∏
n
=
1
∞
(
1
+
x
y
n
(
x
+
y
+
n
)
)
−
1
,
B
(
x
,
y
)
=
1
y
∑
n
=
0
∞
(
−
1
)
n
(
y
)
n
+
1
n
!
(
x
+
n
)
g
d
z
i
e
(
x
)
n
=
x
(
x
−
1
)
(
x
−
2
)
…
(
x
−
n
+
1
)
.
{\displaystyle {\begin{aligned}\mathrm {B} (x,y)&=2\int _{0}^{\pi /2}(\sin \theta )^{2x-1}(\cos \theta )^{2y-1}\,d\theta \,,&&\operatorname {Re} (x)>0,\ \operatorname {Re} (y)>0\,,\\[6pt]\mathrm {B} (x,y)&=\int _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt\,,&&\operatorname {Re} (x)>0,\ \operatorname {Re} (y)>0\,,\\[6pt]\mathrm {B} (x,y)&=\sum _{n=0}^{\infty }{\frac {\binom {n-y}{n}}{x+n}}\,,\\[6pt]\mathrm {B} (x,y)&={\frac {x+y}{xy}}\prod _{n=1}^{\infty }\left(1+{\frac {xy}{n(x+y+n)}}\right)^{-1},\\[6pt]\mathrm {B} (x,y)&={\frac {1}{y}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(y)_{n+1}}{n!(x+n)}}&&\mathrm {gdzie} \quad (x)_{n}=x(x-1)(x-2)\ldots (x-n+1)\,.\end{aligned}}}
Gdy
x
∈
N
{\displaystyle x\in \mathbb {N} }
y
∈
N
{\displaystyle y\in \mathbb {N} }
:
B
(
x
,
y
)
=
(
x
−
1
)
!
(
y
−
1
)
!
(
x
+
y
−
1
)
!
.
{\displaystyle \mathrm {B} (x,y)={\frac {(x-1)!\,(y-1)!}{(x+y-1)!}}.}
Funkcja Beta spełnia wiele ciekawych tożsamości , m.in. są to:
B
(
x
,
y
)
=
B
(
x
,
y
+
1
)
+
B
(
x
+
1
,
y
)
,
{\displaystyle \mathrm {B} (x,y)=\mathrm {B} (x,y+1)+\mathrm {B} (x+1,y),}
B
(
x
+
1
,
y
)
=
B
(
x
,
y
)
⋅
x
x
+
y
,
{\displaystyle \mathrm {B} (x+1,y)=\mathrm {B} (x,y)\cdot {\frac {x}{x+y}},}
B
(
x
,
y
)
⋅
(
t
↦
t
+
x
+
y
−
1
)
=
(
t
→
t
+
x
−
1
)
∗
(
t
→
t
+
y
−
1
)
g
d
z
i
e
x
⩾
1
,
y
⩾
1
,
{\displaystyle \mathrm {B} (x,y)\cdot \left(t\mapsto t_{+}^{x+y-1}\right)={\Big (}t\to t_{+}^{x-1}{\Big )}*{\Big (}t\to t_{+}^{y-1}{\Big )}\quad \mathrm {gdzie} \quad x\geqslant 1,y\geqslant 1,}
B
(
x
,
y
)
⋅
B
(
x
+
y
,
1
−
y
)
=
π
x
sin
(
π
y
)
.
{\displaystyle \mathrm {B} (x,y)\cdot \mathrm {B} (x+y,1-y)={\frac {\pi }{x\sin(\pi y)}}.}
Niekompletna funkcja beta
edytuj
Niekompletna funkcja beta to uogólnienie funkcji beta zdefiniowane następująco[2]
B
(
x
;
a
,
b
)
=
∫
0
x
t
a
−
1
(
1
−
t
)
b
−
1
d
t
.
{\displaystyle \mathrm {B} (x;\,a,b)=\int _{0}^{x}t^{a-1}\,(1-t)^{b-1}\,dt.}
Regularyzowana niekompletna funkcja beta jest zdefiniowana jako iloraz niekompletnej funkcji beta i (kompletnej) funkcji beta[2]
I
x
(
a
,
b
)
=
B
(
x
;
a
,
b
)
B
(
a
,
b
)
.
{\displaystyle I_{x}(a,b)={\frac {\mathrm {B} (x;\,a,b)}{\mathrm {B} (a,b)}}.}
Regularyzowana niekompletna funkcja beta jest dystrybuantą rozkładu beta .
![{\displaystyle {\begin{aligned}\mathrm {B} (x,y)&=2\int _{0}^{\pi /2}(\sin \theta )^{2x-1}(\cos \theta )^{2y-1}\,d\theta \,,&&\operatorname {Re} (x)>0,\ \operatorname {Re} (y)>0\,,\\[6pt]\mathrm {B} (x,y)&=\int _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt\,,&&\operatorname {Re} (x)>0,\ \operatorname {Re} (y)>0\,,\\[6pt]\mathrm {B} (x,y)&=\sum _{n=0}^{\infty }{\frac {\binom {n-y}{n}}{x+n}}\,,\\[6pt]\mathrm {B} (x,y)&={\frac {x+y}{xy}}\prod _{n=1}^{\infty }\left(1+{\frac {xy}{n(x+y+n)}}\right)^{-1},\\[6pt]\mathrm {B} (x,y)&={\frac {1}{y}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(y)_{n+1}}{n!(x+n)}}&&\mathrm {gdzie} \quad (x)_{n}=x(x-1)(x-2)\ldots (x-n+1)\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e06112070f4e8accdd8255f3c5aecc12579a5b5c)
