Automat skończony

Automat skończony (ang. finite state machine) – abstrakcyjny, matematyczny, iteracyjny model obliczeń w teorii automatów oparty na tablicy dyskretnych przejść między jego kolejnymi stanami, do opisu których służy diagram stanów.

Przykład automatu skończonego

Ze względu na charakter przejść między stanami, wyróżnia się deterministyczne i niedeterministyczne automaty skończone. Maszyna Turinga jest generalizacją automatu skończonego operującą na nieskończonej pamięci.

Automaty skończone są wykorzystywane w tworzeniu systemów komputerowych i opisie układów dynamicznych. Zachowania automatów skończonych można zaobserwować w wielu urządzeniach współczesnego społeczeństwa, które wykonują z góry ustaloną sekwencję działań w zależności od sekwencji zdarzeń, z którymi są prezentowane. Najprostszymi przykładami są automaty sprzedające produkty po zdeponowaniu odpowiedniej kombinacji monet, windy, których kolejność postojów jest określona przez piętra wybierane przez pasażerów, sygnalizacja świetlna, która zmienia sekwencję, gdy czekają samochody, oraz zamki szyfrowe, które wymagają wprowadzanie sekwencji liczb we właściwej kolejności.

Przykład automatu skończonego

Na ilustracji przedstawiono prosty automat skończony mogący przyjąć jeden z dwóch stanów – $S_{1}$ lub $S_{2}.$ Automat zaczyna pracę od stanu $S_{1}$ i zachowuje się w sposób stabilny (nie zmienia stanu) tak długo, jak długo na wejściu otrzymuje liczby $1.$ Każde napotkane na wejściu 0 zmienia stan układu na przeciwny. Proces ten można przedstawić również za pomocą listy przejść

stan startowy – $S_{1}$

$S_{1}\to ^{1}S_{1}$

$S_{1}\to ^{0}S_{2}$

$S_{2}\to ^{1}S_{2}$

$S_{2}\to ^{0}S_{1},$

jak i tabeli

	0	1
S1	S2	S1
S2	S1	S2

Za pomocą tego automatu możemy badać czy liczność zer w danym ciągu jest parzysta czy też nie. Gdy na wejściu pojawi się nieparzysta liczba zer automat przyjmie stan $S_{2}.$ W każdym innym wypadku automat przyjmie stan $S_{1}.$

Przykład wykonania dla ciągu wejściowego 0011010:

liczba na wejściu	(start)	0	0	1	1	0	1	0
stan automatu	S1	S2	S1	S1	S1	S2	S2	S1

Automat zakończył pracę w stanie $S_{1},$ co oznacza parzystą liczbę 0 w ciągu wejściowym.

Przykład 2

Automat badający podzielność liczby wejściowej przez 3

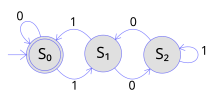
Przedstawiony jako ilustracja we wstępie do artykułu automat jest w stanie badać podzielność liczby wejściowej przez $3.$ Automat zaczyna pracę od stanu $S_{0},$ i po przeczytaniu każdej cyfry przechodzi do stanu $S_{j}$ (gdzie: $j=0,1,2$)

stan startowy – $S_{0}$

$S_{0}\to ^{0}S_{0}$

$S_{0}\to ^{1}S_{1}$

$S_{1}\to ^{0}S_{2}$

$S_{1}\to ^{1}S_{0}$

$S_{2}\to ^{0}S_{1}$

$S_{2}\to ^{1}S_{2}.$

Proces ten można także zapisać w postaci tabeli:

	0	1
S0	S0	S1
S1	S2	S0
S2	S1	S2

Przykład 3

Automat badający podzielność liczby wejściowej przez 4

Na ilustracji po prawej stronie przedstawiono prosty automat skończony badający podzielność liczby wejściowej przez $4.$ Automat zaczyna pracę od stanu $S_{0},$ i po przeczytaniu każdej cyfry przechodzi do stanu $S_{j}$ (gdzie: $j=0,1,2$)

stan startowy – $S_{0}$

$S_{0}\to ^{0}S_{0}$

$S_{0}\to ^{1}S_{1}$

$S_{1}\to ^{0}S_{2}$

$S_{1}\to ^{1}S_{1}$

$S_{2}\to ^{0}S_{0}$

$S_{2}\to ^{1}S_{1}.$

Proces ten można także zapisać w postaci tabeli:

	0	1
S0	S0	S1
S1	S2	S1
S2	S0	S1

Zobacz też

• automat Büchiego
• automat Moore’a
• automat Mealy’ego
• deterministyczny automat skończony
• niedeterministyczny automat skończony

Linki zewnętrzne

• Automaton, finite (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2024-10-05].