Łączny rozkład prawdopodobieństwa

Łączny rozkład prawdopodobieństwa (rzadziej wspólny rozkład prawdopodobieństwa, ang. joint probability distribution) – rodzaj rozkładu prawdopodobieństwa, który zmiennym losowym X, Y, .... przypisuje prawdopodobieństwo, iż zmienne X, Y, .... przyjmą określone wartości (ciągłe lub dyskretne, należące do specyficznych dla każdej z nich zbiorów wartości).

Czarne punkty uzyskane z pomiaru dwóch zmiennych losowych X, Y – większej gęstości punktów w pobliżu danego punktu (x, y) odpowiada większe łączne prawdopodobieństwo, że X przyjmie wartość w pobliżu x, a Y w pobliżu y. Pokazano też rozkłady brzegowe P(X=x) oraz P(Y=y).

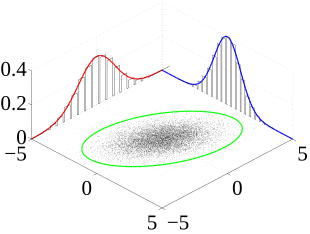
Jeśli mamy tylko dwie zmienne losowe, to rozkład nazywamy dwuwymiarowym, a dla większej liczby zmiennych losowych rozkład nazywamy wielowymiarowym.

Łączny rozkład prawdopodobieństwa może zostać wyrażony także jako łączna dystrybuanta, łączna funkcja gęstości prawdopodobieństwa (w przypadku zmiennych ciągłych) lub łączna funkcja masy prawdopodobieństwa (w przypadku zmiennych dyskretnych). Te z kolei mogą być wykorzystywane do znalezienia dwóch innych rodzajów rozkładów: rozkładu brzegowego (czyli rozkładu prawdopodobieństwa dla jakiejś jednej zmiennej losowej bez odniesienia do pozostałych zmiennych) oraz rozkładu warunkowego (czyli rozkładu prawdopodobieństwa dla wybranego podzbioru zmiennych losowych przy ustalonych wartościach pozostałych zmiennych).

Przykład

Rozważmy rzut sześcienną kostką do gry i skonstruujmy następujące zmienne: A = 1, jeśli wypadnie liczba parzysta (2, 4 lub 6), oraz A = 0, jeśli wypadnie liczba nieparzysta (1, 3 lub 5). Analogicznie, B = 1, jeśli wypadnie liczba pierwsza (2, 3 lub 5), oraz B = 0, jeśli wypadnie inna liczba (1, 4 lub 6).

	1	2	3	4	5	6
A	0	1	0	1	0	1
B	0	1	1	0	1	0

Wtedy łączny rozkład prawdopodobieństwa dla A i B, wyrażony jako funkcja masy prawdopodobieństwa, wynosi

$\mathrm {P} (A=0,B=0)=P\{1\}={\frac {1}{6}},$

$\mathrm {P} (A=1,B=0)=P\{4,6\}={\frac {2}{6}},$

$\mathrm {P} (A=0,B=1)=P\{3,5\}={\frac {2}{6}},$

$\mathrm {P} (A=1,B=1)=P\{2\}={\frac {1}{6}}.$

Ważne rodzaje rozkładów

Nazwanymi przykładami rozkładów łącznych są: wielowymiarowy rozkład normalny, rozkład wielomianowy, ujemny rozkład wielomianowy, wielowymiarowy rozkład hipergeometryczny i rozkład eliptyczny.

Dystrybuanta

Łączny rozkład prawdopodobieństwa dla pary zmiennych losowych może być wyrażona w terminie ich dystrybuanty:

$F(x,y)=P(X\leqslant x,Y\leqslant y).$

Funkcja gęstości lub funkcja masy

Rozkłady dyskretne

Łączna funkcja masy prawdopodobieństwa dla dwóch zmiennych losowych dyskretnych jest równa

${\begin{aligned}\mathrm {P} (X=x\ \mathrm {i} \ Y=y)=\mathrm {P} (Y=y\mid X=x)\cdot \mathrm {P} (X=x)=\mathrm {P} (X=x\mid Y=y)\cdot \mathrm {P} (Y=y)\end{aligned}}.$

Łączny rozkład prawdopodobieństwa $n$ zmiennych losowych dyskretnych $X_{1},X_{2},\dots ,X_{n}$ jest równy

${\begin{aligned}\mathrm {P} (X_{1}=x_{1},\dots ,X_{n}=x_{n})={}&\mathrm {P} (X_{1}=x_{1})\\\times \ &\mathrm {P} (X_{2}=x_{2}\mid X_{1}=x_{1})\\\times \ &\mathrm {P} (X_{3}=x_{3}\mid X_{1}=x_{1},X_{2}=x_{2})\\\times \ &\ldots \\\times \ &P(X_{n}=x_{n}\mid X_{1}=x_{1},X_{2}=x_{2},\dots ,X_{n-1}=x_{n-1}).\end{aligned}}$

Tożsamość ta jest znana w teorii prawdopodobieństwa pod nazwą reguła łańcuchowa.

Ponieważ są to prawdopodobieństwa, w przypadku dwóch zmiennych mamy

$\sum _{i}\sum _{j}\mathrm {P} (X=x_{i}\ \mathrm {i} \ Y=y_{j})=1,$

które uogólniają $n$ zmiennych losowych dyskretnych $X_{1},X_{2},\dots ,X_{n}$ do

$\sum _{i}\sum _{j}\ldots \sum _{k}\mathrm {P} (X_{1}=x_{1i},X_{2}=x_{2j},\dots ,X_{n}=x_{nk})=1.$

Rozkłady ciągłe

Łączna funkcja gęstości prawdopodobieństwa $f_{X,Y}(x,y)$ dla zmiennych losowych ciągłych wynosi

$f_{X,Y}(x,y)=f_{Y\mid X}(y|x)f_{X}(x)=f_{X\mid Y}(x\mid y)f_{Y}(y),$

gdzie $f_{Y\mid X}(y\mid x)$ i $f_{X\mid Y}(x\mid y)$ dają rozkład warunkowy, gdzie $Y$ równa się $X=_{x},$ a $X$ równa się $Y=_{y},$ natomiast $f_{X}(x)$ i $f_{Y}(y)$ dają rozkład brzegowy odpowiednio dla $X$ i $Y.$

Ponieważ są to rozkłady prawdopodobieństwa, po połączeniu ich uzyskamy:

$\int _{x}\int _{y}f_{X,Y}(x,y)\;dy\;dx=1.$

Łączny rozkład dla zmiennych niezależnych

Jeśli dla zmiennych losowych dyskretnych $P(X=x\ {\text{i}}\ Y=y)=P(X=x)\cdot P(Y=y)$ dla wszystkich $x$ i $y$ całkowicie zmiennych losowych ciągłych $f_{X,Y}(x,y)=f_{X}(x)\cdot f_{Y}(y)$ dla wszystkich $x$ i $y,$ wtedy $x$ i $y$ są uważane za niezależne. Oznacza to, że pozyskiwanie informacji o wartości jednej lub więcej zmiennych losowych prowadzi do rozkładu warunkowego innych zmiennych, który jest identyczny do rozkładu bezwarunkowego (brzegowego), zatem nie zmienne są źródłem informacji o zmiennych losowych.

Łączny rozkład dla zmiennych zależnych warunkowo

Jeśli podzbiór $A$ zmiennych $X_{1},\dots ,X_{n}$ jest warunkowo zależny od innego podzbioru $B$ tych zmiennych, wówczas łączny rozkład $P(X_{1},\dots ,X_{n})$ można zapisać jako $P(B)\cdot P(A\mid B)$. Dzięki temu rozkład ten można skutecznie przedstawić za pomocą mniejszych wielowymiarowych rozkładów prawdopodobieństwa $P(B)$ oraz $P(A\mid B)$. Zależności warunkowe (ang. conditional independence relations) tego typu mogą być modelowane za pomocą sieci bayesowskich.

Zobacz też

• kopula (matematyka)
• prawdopodobieństwo warunkowe

Bibliografia

• „Joint distribution”, Encyclopedia of Mathematics, ISBN 978-1-55608-010-4.
• „Multi-dimensional distribution”, Encyclopedia of Mathematics, ISBN 978-1-55608-010-4.
• Joint continuous density function
• Eric W.E.W. Weisstein Eric W.E.W., Joint Distribution Function, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).